1) Compton camera
康普顿成像装置
1.
A Compton camera consisting of two position sensitive germanium detectors is proposed for multitracer technique.
提出了一个由位置灵敏高纯锗探测器组成、用于多重示踪技术的康普顿成像装置。
2) Compton scatter imaging
康普顿散射成像
1.
The authors introduce the main applications of Compton scattering-density measurement,thickness measurement and flaw detection with Compton scatter imaging and other ap.
介绍了康普顿散射在密度测量、厚度测量方面的应用,讨论了利用康普顿散射成像来进行缺陷检测等方面的问题,同时介绍了康普顿散射在安全检测、医药技术、食品加工等其他领域的应用。
2.
In the field of Compton scatter imaging, the problem of how to image a large-scale object is still not fully settled.
在现有的康普顿散射成像技术中 ,如何对大型物体进行成像的问题始终没有得到充分解决。
3) Compton back scattering tomography
康普顿背散射成像
1.
The transmitting computed tomography and Compton back scattering tomography were used especially.
本文选用不同的方法对两个导线线圈进行了射线检测,主要采用透射式工业CT检测和康普顿背散射成像检测两种射线层析检测方法,有效检测了导线线圈内部的缺陷情况,并指出射线层析检测作为一项新技术和新手段,可充分应用在航天产品的无损检测中。
4) the compton back-scatter imaging tomography
康普顿背散射成像检测
5) anti-Compton
反康普顿
1.
Ten years running of a set of low background anti-Compton HPGe γ-ray spectrometer;
一套低本底反康普顿HPGe γ谱仪十年运行回顾
2.
This paper analyses the integral background of a low-background anti-Compton HPGeγ-ray spectrometer by measuring the integral background under three kinds of conditions: no shield,steel-lead complex shield,and steel-lead complex shield plus anti-coincidence.
本文对一套低本底反康普顿HPGeγ谱仪系统的积分本底进行了实验研究,测量了谱仪系统在无屏蔽、屏蔽室以及屏蔽室加反符合三种条件下的积分本底。
3.
This paper introduces the anti-coincidence working principle and composing of the low-background anti-Compton HPGe γ ray spectrometer.
介绍了反康普顿HPGeγ谱仪系统的结构组成和井型反符合工作原理,对系统在有无反符合测量条件、源与环探测器相对距离以及源强对峰康比的影响进行了实验研究。
补充资料：康普顿散射
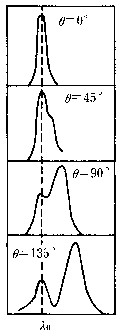
| 康普顿散射 Compton scattering 物质对X射线的散射。又称康普顿效应。康普顿效应可归结为：①设入射X射线的波长为λ0，在散射光中除原波长的谱线外还出现波长λ＞λ0的谱线。②波长差Δλ＝λ－λ0随散射角θ（散射光与入射光间的夹角）的增加而增加；散射光中波长为λ的谱线强度随θ的增加而增强（图1）。
③对不图1同元素的散射物质，同一散射角时的波长差Δλ均相同；波长为λ的谱线强度随散射元素的原子序数的增加而减弱（图2）。
康普顿效应不能用经典的波动理论来解释。1923年A.H.康普顿利用光子概念图2把上述散射效应看成是X光光子与散射物质中静止自由电子作弹性碰撞的结果，从而对康普顿散射作出了正确的解释。光子作为微粒，既有能量又有动量；散射物质中的价电子被束缚较弱可近似看作是自由电子，其能量远比X光子的能量要小，故可看作是静止的；X光子与自由电子作弹性碰撞时遵守动量守恒和能量守恒定律。根据以上考虑可导出波长差Δλ与散射角θ间的关系为 Δλ＝  （1－cosθ）＝λc（1－cosθ），式中h为普朗克常数；m0为电子的静质量；c为真空中的光速；λc＝2。42631×10-2埃是一普适常数，称为康普顿波长。康普顿效应为光的量子性提供了有力证据。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条