1) M/M/n/n/m queuing model


M/M/n/n/m排队模型
2) M/M/n queueing model


M/M/n排队模型
1.
In this paper, the dynamic M/M/n queueing model is discussed, By using the c 0 -Semigroup theory, the existence of a unique dynamic positive solution of M/M/n model is given.
文章讨论动态 M/M/n排队模型 ,运用算子半群理论证明了该模型动态正解的存在唯一性 。
2.
The dynamic M/M/n queueing model with variable import rate is discussed using the C0-semigroup theory,the existence of an unique dynamic positive solution of M/M/n queueing model with variable import rate is given.
讨论动态具有可变输入率的M/M/n排队模型,运用算子半群理论证明该模型动态正解的存在唯一性,并进一步表明0是系统的一个本征值,相应的本征函数为系统的一个定态正解,系统的动态正解强渐近稳定到定态解。
3) M/M/n/m model


M/M/n/m排队模型
4) E k/M/n queuing model


Ek/M/n排队模型
5) M/M/n/n/m model


M/M/n/n/m模型
6) M/M/n model


M/M/n模型
1.
By using the whole probability principle of random modeling,an ordinary differential equation on the M/M/n model with variable import rate is deduced,which provides a basis for the theoretical analysis on the M/M/n model s dynamic solution and stability.
利用随机建模的全概率法则推导了具有可变输入率的M/M/n模型的常微分方程形式,为从理论上分析该模型动态解及其稳定性奠定了基础。
2.
By the use of total probability principle, we obtain an ordinary differential equation of the {M/M/n} model with impatient customer, presenting the base on the analysis of the M/M/n model′s dynamic solution and stability.
本文针对实际生活中大量存在的排队现象:队列中具有不耐烦顾客,利用随机建模的全概率法则推导了具有不耐烦顾客的M/M/n模型的常微分方程形式,为从理论上分析该模型动态解及其稳定性奠定了基础。
补充资料:AutoCad 教你绘制三爪卡盘模型,借用四视图来建模型
小弟写教程纯粹表达的是建模思路,供初学者参考.任何物体的建摸都需要思路,只有思路多,模型也就水到渠成.ok废话就不说了.建议使用1024X768分辨率
开始
先看下最终效果

第一步,如图所示将窗口分为四个视图

第二步,依次选择每个窗口,在分别输入各自己的视图

第三步,建立ucs重新建立世界坐标体系,捕捉三点来确定各自的ucs如图
第四步,初步大致建立基本模型.可以在主视图建立两个不同的圆,在用ext拉升,在用差集运算.如图:

第五步:关键一步,在此的我思路是.先画出卡爪的基本投影,在把他进行面域,在进行拉升高度分别是10,20,30曾t形状.如图:

第六步:画出螺栓的初步形状.如图

第七步:利用ext拉升圆,在拉升内六边形.注意拉升六边行时方向与拉升圆的方向是相反的.
之后在利用差集运算


第八步:将所得内螺栓模型分别复制到卡爪上,在利用三个视图调到与卡爪的中心对称.效果如图红色的是螺栓,最后是差集
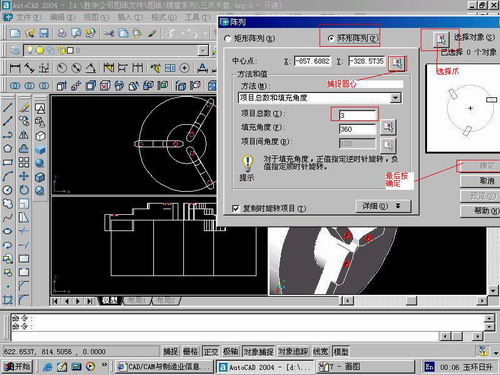
第九步:阵列

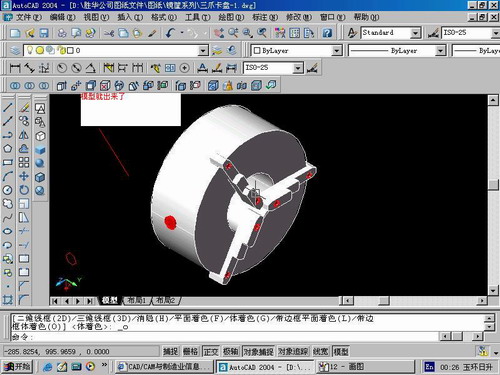
第10步.模型就完成了

来一张利用矢量处理的图片

说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条