1) multiple-failure-hypothesis based testing


多重故障假设检验
1.
According to Kalman filter and multiple-failure-hypothesis based testing,the sensor failures are detected,isolated and accommodated in turbofan engine control system.
研究利用卡尔曼滤波器及多重故障假设检验方法来检测某发动机控制系统传感器硬、软故障,并实现故障传感器的输出重构。
2) multiple hypothesis testing


多重假设检验
1.
On the basis of multiple hypothesis testing,we proposed a feature weighted naive Bayesian algorithm,which outputs many sets of feature words by means of feature selection,and assigns a coefficient to each set of feature words which is used to construct the classifier in terms of the error rate of multiple hypothesis testing.
提出一种基于多重假设检验的特征加权朴素贝叶斯分类算法,该算法通过特征选择方法得到多个特征词集合,再按多重假设检验错误率为每个特征词集合配以不同的权重系数并参与到分类器的构建中。
3) multihypothesis test


多假设检验
4) Multistage hypothesis


多级假设检验
5) multiple hypotheses testing


多元假设检验
1.
The theory of multiple hypotheses testing is one of the difficult and important contents in the teaching of random signal analysis and processing.
多元假设检验理论是随机信号分析与处理课程教学中的难点和重点内容。
6) malfunction check


故障检验
补充资料:假设检验
| 假设检验 hypothesis testing 一种基本的统计推断形式。又称统计假设检验。数理统计学的一个重要分支。假设是指关于总体分布的一项命题 。例如 ,一群人的身高服从正态分布N(μ ,σ2),则命题“这群人的平均身高μ≤1.70(米)”是一个假设 。又如,有一批产品,其废品率为p,则“废品率p≤0.03”这个命题也是一个假设。假设是否正确, 要用从总体中抽出的样本进行检验,与此有关的理论和方法,构成假设检验的内容。 设A是关于总体分布的一项命题,所有使命题A 成立的总体分布构成一个集合H0,称为原假设(常简称假设)。使命题A不成立的所有总体分布构成另一个集合H1 ,称为各择假设。如果H0可以通过有限个实参数来描述,则称为参数假设,否则称为非参数假设(见非参数统计)。如果H0(或H1)只包含一个分布,则称原假设(或备择假设)为简单假设,否则为复合假设。对一个假设H0进行检验,就是要制定一个规则,使得有了样本以后 ,根据这个规则可以决定是接受它(承认命题A正确),还是拒绝它(否认命题A正确)。这样, 所有可能的样本所组成的空间(称为样本空间),被划分为两部分  A和 A和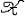 R( R(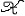 A的补集),当样本x∈ A的补集),当样本x∈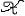 R时,接受假设H0 ;当x∈ R时,接受假设H0 ;当x∈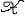 R时,拒绝H0 。集合 R时,拒绝H0 。集合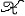 R常称为检验的拒绝域, R常称为检验的拒绝域,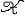 A称为接受域。因此选定一个检验法 ,也就选定一个拒绝域 ,故常把检验法本身与拒绝域 A称为接受域。因此选定一个检验法 ,也就选定一个拒绝域 ,故常把检验法本身与拒绝域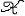 R 等同起来。 R 等同起来。J.奈曼与E.S.皮尔森合作,从1928年开始,对假设检验提出了一项系统的理论。他们认为,在检验一个假设H0时可能犯两类错误: 第一类错误是真实情况为H0成立,但判断H0不成立,犯了“以真为假”的错误。第二类错误是H0 实际不成立,但判断它成立,犯了“以假为真”的错误。通常人们不希望轻易拒绝H0。例如工厂的产品一般是合格的 ,出厂进行抽样检查时不希望轻易地被认为不合格,即犯第一类错误的概率不能太大,于是在限定犯第一类错误的概率不超过某个指定值a(称为检验水平)的条件下,寻求犯第二类错误尽可能小的检验方法。 基于奈曼-皮尔森理论及统计决策理论,提出了一些优良性准则,来比较为检验同一假设而提出的各种检验。较重要的有一致最大功效(UMP)准则和无偏性准则, 把统计决策理论中容许性、同变性、贝叶斯决策、最小化最大等概念引进到假设检验中来,得到容许检验、同变检验、贝叶斯检验和最小化最大检验等。寻求在一定准则下的最优检验是十分困难的,何况这种最优检验有时并不存在。于是提出了若干依据直观的推理法,得到相应的拒绝域,其中最重要的是似然比法。 似然比检验是运用与最大似然法类似的原理,得到似然比检验法。用似然比法导出的重要检验有:①U检验。若总体服从正态分布,方差已知,检验总体均值是否等于(大于等于或小于等于)某个值时,使用U检验。②t检验。若总体服从正态分布,方差未知,检验总体均值是否等于(大于等于或小于等于)某个值时,使用t检验。③F检验。若两个总体均服从正态分布,检验这两个总体的方差是否相等(大于等于或小于等于)时,使用F检验。在方差分析中广泛使用F检验。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条