1) optimum fractal dimension
最佳分形维数
1.
When it is used in the running-in process,the model can predict optimum fractal dimension precisely.
将该模型用于销 盘磨合磨损试验, 对最佳分形维数进行了准确预测。
2) optimal dimension
最佳维数区
1.
The optimal prediction value and the optimal dimension are calculated and the post-error method is used to examine the precision of the model.
在分析了传统GM(1,1)模型和无偏灰色预测模型的基础上提出了无偏等维新息预测模型,通过运算得出最佳预测值以及预测的最佳维数区,并采用后验差方法对模型的精度进行检验。
3) optimal class number
最佳分类数
1.
Based on this index system with the use of MATLAB platform,the author applied fuzzy cluster analysis and structure F-statistics to determine the optimal class number for the six categories of classification,using factor analysis of the results of a simple description for the comprehensive construction of a well-off society t.
以树立科学发展观为出发点,对2004年全国35个主要城市选取了7大类15项指标作为小康水平评价体系,依据此指标体系,基于matlab平台,进行模糊聚类分析,并构造F统计量确定最佳分类数为6类,借助因子分析对结果进行了简单说明,为全面建设小康社会提供科学依据。
4) Optimal Embedding Dimension
最佳嵌入维数
5) optimum deformation parameter
最佳变形参数
6) optimum building shape coefficient
最佳体形系数
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 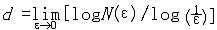 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条