1) (idempotent-separated)good congruence


(幂等可分)良同余
2) idempotent-separating congruence


幂等元分离同余
1.
The maximum idempotent-separating congru-ence is extremely important in studying the structure of fundamental regular semigroup and regular semigroup with inverse transversals,so an equivalent depict is given of the maximum idempotent-separating congruence on regular semigroups .
最大幂等元分离同余在研究具有逆断面的基础正则半群以及正则半群的结构时起到至关重要的作用,给出了具有逆断面的正则半群的最大幂等元分离同余的一种等价刻画。
3) idempotent-seperating congruences


幂等分离同余
4) idempotent congruent number


幂等同余数
1.
All the idempotent congruent numbers of any integer which is greater than 1 were given out.
给出了以任意大于1的整数为模的所有幂等同余数,以及它们的数目;应用幂等同余数简化了任何整数幂的余数的计算问
5) idempotent –pure congruence


幂等纯同余
6) the maximum idempotent-separating congruence


极大幂等元分离同余
补充资料:幂
| 幂 power 表示一个数自乘若干次的形式。ab称为a的b次幂。其中a称为这个幂的底数,b称为这个幂的指数。这里乘方的含义随着指数b所在范围不同而有不同的规定。① 当b是正整数n时,an称为正整数指数幂,表示n个a连乘的结果,即 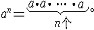 ②当b是负整数-n且a≠0时,a-n称为负整数指数幂,规定 ②当b是负整数-n且a≠0时,a-n称为负整数指数幂,规定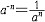 ,即 ,即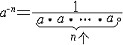 ③当b=0且 ③当b=0且 ≠0时, ≠0时, 0称为 0称为 的零次幂,规定 的零次幂,规定 0=1。④ 当b为正分数m/n(m,n都是正整数,且n>1)时,限定 0=1。④ 当b为正分数m/n(m,n都是正整数,且n>1)时,限定 ≥0,规定 ≥0,规定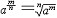 ,称为a的正分数指数幂 。⑤当b是负分数-(m ,n为正整数,且n>1)时,限定 ,称为a的正分数指数幂 。⑤当b是负分数-(m ,n为正整数,且n>1)时,限定 >0,规定 >0,规定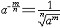 ,称为 ,称为 的负分数指数幂。⑥当b是无理数 的负分数指数幂。⑥当b是无理数 ,且 ,且 >0时,aa称为a的无理数指数幂,对正无理数 >0时,aa称为a的无理数指数幂,对正无理数 ,取有理数列{ ,取有理数列{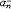 }和{ }和{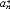 }, }, 和 和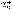 分别是 分别是 的精确到1/10n的不足近似值和过剩近似值 。有理数指数幂 的精确到1/10n的不足近似值和过剩近似值 。有理数指数幂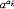 和 和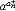 已经有了定义,于是规定 已经有了定义,于是规定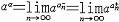 ,即aa用两个数列{ ,即aa用两个数列{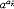 }和{ }和{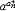 }的共同极限确定。对于负无理数- }的共同极限确定。对于负无理数- ,规定 ,规定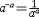 。 。这样,对幂指数由正整数到无理数各种情况,幂的概念都有了规定。从而,任意实数指数幂都有确切的含义。实数指数幂的运算法则有:①  a· a· β= β= a +β;②( a +β;②( a) β= a) β= aβ;③( aβ;③( b)a= b)a= aba。式中 aba。式中 >0,b>0; >0,b>0; ,β为任意实数,这与正整数指数幂的运算法则相同。 ,β为任意实数,这与正整数指数幂的运算法则相同。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条