1) weighted eigenvector Least Square Support Vector Machine


加权特征向量最小二乘支持向量机
1.
This paper present the online weighted eigenvector Least Square Support Vector Machine(WEVLS-SVM) technique to identify the structural damage based on the sequential incremental Least Square Support Vector Machine(SILS-SVM) technique.
在增量式最小二乘支持向量机(SILS-SVM)方法的基础上,提出了加权特征向量最小二乘支持向量机(WEVLS-SVM)在线结构损伤识别方法。
2) weighted LS-SVM


加权最小二乘支持向量机
1.
In order to increase the robustness of LS-SVM, weighted LS-SVM is introduced.


为了提高最小二乘支持向量机的鲁棒性,介绍了加权最小二乘支持向量机,给出了确定加权向量的一般方法。
3) least squares support vector machine


最小二乘支持向量机
1.
Application of least squares support vector machine within evidence framework in PTA process;
基于证据框架的最小二乘支持向量机在精对苯二甲酸生产中的应用
2.
Pressure sensor temperature compensation based on least squares support vector machine;


基于最小二乘支持向量机的压力传感器温度补偿
3.
Sparse least squares support vector machine;


稀疏最小二乘支持向量机
4) least square support vector machine


最小二乘支持向量机
1.
Forecast of water inrush from coal floor based on least square support vector machine;


基于最小二乘支持向量机的煤层底板突水量预测
2.
Outliers detection in time series of measured data based on least square support vector machine algorithm;
基于最小二乘支持向量机算法的测量数据时序异常检测方法
3.
Image registration based on least square support vector machine;


基于最小二乘支持向量机的图像配准研究
5) least squares support vector machines


最小二乘支持向量机
1.
Coal washery daily water consumption short-term prediction based on least squares support vector machines;
基于最小二乘支持向量机的选煤厂日用水量短期预测
2.
Selection of suitable 3D terrain matching field based on least squares support vector machines;
基于最小二乘支持向量机的三维地形匹配选择
3.
Thermal error prediction of numerical control machine tools based on least squares support vector machines;
基于最小二乘支持向量机的数控机床热误差预测
6) LS-SVM


最小二乘支持向量机
1.
Prediction of hydrogen content in molten aluminum based on LS-SVM;


利用最小二乘支持向量机预测铝熔体氢含量
2.
Time Series Prediction Based on LS-SVM;


基于最小二乘支持向量机的小样本建模方法研究
3.
Research on vibration fault diagnosis of hydro-turbine generating unit based on LS-SVM and information fusion technology;
基于最小二乘支持向量机和信息融合技术的水电机组振动故障诊断研究
补充资料:向量
| 向量 vector 一种既有大小又有方向的量。又称矢量。在理论和实际中均广泛应用。速度、加速度、力等都是向量。 从空间中任一点出发,作一直线l,在l上取一点B,则有向线段AB就代表一个向量,记作AB或a(图1),它的大小是线段AB的长度,也称为模或绝对值,记作|a|=a,方向就是l的方向。如果另有A¢B ¢||蜛B,且指向相同,长度相等 ,就说向量AB=A¢B ¢。这种起点可以自由改变的向量常称为自由向量,当点B与A重合时,称为零向量,记作0,它的模为0,方向不确定。模为1的向量称为单位向量,向量a=b,当且仅当它们的方向相同且模相等,非零向量a与b平行或重合记为a∥b。-a是指与a方向相反模相等的向量。a与b垂直,如果它们所在直线垂直,记为a⊥b,除上面这种几何表示法以外,还常用代数方法表示向量,这种方法便于运算,便于进行有关性质的讨论。具体做法如下:在空间取定一右手坐标系(图2),把给定向量的起点放在原点,其终点为P,则a=OP,设P点在坐标系下的坐标为(x,y,z),则a={x,y,z}就是向量a的代数表示,分别称x,y,z为向量a在x轴、y轴、z轴上的分量,零向量o的三个分量均为0,即o={0,0,0}。下面介绍向量的数乘、加减法、内积、外积和混合积等运算。这些运算在代数表示法下简单明了,在几何表示法下直观,各有长处。数乘:向量a与数c相乘,得到向量ca,其模为|ca|=|c||a|,当c>0时,方向与a相同,c<0时,方向与a相反,c=0时,方向不定,得到零向量。若用代数表示法,a={x,y,z},则 ca={cx,cy,cz}。数乘满足结合律:b(ca)=(bc)a。加法:将a=OA,b=OB取在同一起点O(图3),再以OA,OB为边作平行四边形OACB,定义向量OC=c为向量a与b之和。为用代数表示法,a={x1,y1,z1},b={x2,y2,z2},则定义a+b={x1+x2,y1+y2,z1+z2},向量加法满足交换律、结合律和对数乘的分配律。向量的减法可作为加法的逆运算来定义。向量的内积(也称为点积):设a,b均不为零向量,它们的夹角为θ,则定义a·b=|a||b|cosθ,如a、b中有一个为零向量,则定义a·b=0。用代数表示法,当a={x1,y1,z1},b={x2,y2,z2}时,a·b=x1x2+y1y2+z1z2,内积满足交换律、结合律及与数乘的分配律。向量的外积:对于两个不平行的非零向量a、b,定义a×b为向量c,|c|=|a||b||sinθ|,其中θ为a与b的夹角,且c与a、b均垂直,a、b、c的指向构成右手系(图4),因为a×b仍为向量,故外积也称为向量积。用代数表示法时,a×b=c={y1z2-z1y2,z1x2-x1z2,x1y2-y1x2},其中a={x1,y1,z1} ,b={x2,y2,z2},向量的内积与外积间满足关系:(a×b)2=a2b2-(a·b)2 。向量的混合积(a×b)·c ,也记为(a,b,c)。设a={x1,y1,z1},b={x2,y2,z2},c={x3,y3,z3},则 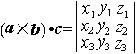
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |