1) ramification dimension
分枝维数
1.
Based on GIS technology,radial dimensions(DL),ramification dimensions(Db) and correlation coefficient(R2) of the distribution of highw.
基于分形理论,以GIS技术为支撑,利用回转半径法测算了广东省全域及其所辖21个地级市公路交通网络半径维数DL、分枝维数Db和对应相关系数R2。
2) branching
分枝
1.
Branching and growth of plantings in fifth year of a seedling seed orchard of Masson pine (Pinus massoniana Lamb.);
马尾松实生种子园五年生的植株生长与分枝(英文)
2.
Discovery and Molecular Tagging of New Earbranching Gene in Natural Barley Mutant;
大麦天然突变体穗分枝新基因的发现及分子标记定位
3.
The morphology and branching behavior of silicon phase in Al-12.
7％Si共晶中硅相的形态与分枝特征。
3) branch
分枝
1.
Curvilinear Equations and Its Goodness of Fit for Characteristics of Plant Growth and Branching;
青蒿株高生长与分枝特性的曲线方程及其拟合性研究
2.
Effects of soil nitrogen availability and clonal integration on the branching behaviors of Zoysia japonica;
土壤氮素有效性与克隆整合性对结缕草分枝行为的影响效应(英文)
3.
There are a lot of burrs and branches after thinning the binary image of the light stripe,which will heavily affect the accuracy of the line-structure-light 3D shape measurement,so burrs and branches must be cut at first.
在采用线结构光进行三维测量的过程中,将光刀图像细化后得到的骨架会出现许多毛刺和分枝,而光刀图像骨架的位置和形状将会直接影响到测量的精度,为了能够得到一条光顺并具有单一连通性的骨架,必须对其进行剪枝处理。
4) bifurcation
分枝
1.
One of the basic problems in bifurcation theory is to understand the way in which horseshoes created.
如何理解smale马蹄的产生是分枝理论的一个基本问题。
2.
The sufficient conditions of the existence of chaotic behaviour and subharmonic bifurcaion hypersubharmonic bifurcation are obtained.
应用Melnikov方法确定出系统产生浑沌及次谐波分枝、超次谐波分枝的某些充分条件,并讨论了从分枝进入浑沌的途径。
3.
Quadric system(Ⅲ) of the formis studied, where b = n =-m/δ, and the existence and uniqueness of limit cycles of the system is proved, their bifurcation behaviour is fully analysed.
研究了二次系统(Ⅲ) 其中b=n=-m/δ,证明了该系统极限环的存在唯一性,讨论了解关于δ的分枝结构,解决了极限环的确切个数和分布问题。
5) Shoot branching
分枝
1.
Shoot branching is one of the most important components of plant architecture, which are mostly determined genetically, and are also partly affected by environmental factors.
植物分枝发育在植物形态建成中具有十分重要的地位,在受遗传决定的同时,也受环境的影响。
2.
The study of molecular mechanism of shoot branching has scientific significance.
了解植物分枝机理不仅具有理论意义,对于农业、林业、果树、蔬菜和花卉等生产实践更具有重要意义。
6) Ramification
分枝
1.
Autolysis and ramification of thermostreptomyces and its interaction with bacteria;
高温链霉菌与细菌的相互作用及其自溶和分枝机制
参考词条
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 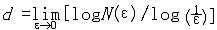 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。