1) continued fractions algorithm
连分数算法
1.
In this paper,based on continued fractions algorithm and branching-bounding algorithm,a new algorithm applied in cutting a long rectangular sheet into several sections is put forward.
本文结合连分数算法,采用分支定界原理提出了一种新的板材分割算法。
3) continuous fraction method
连续分数法
1.
By means of the continuous fraction method, the author obtains the exact solutions of the Schrdinger equation with the potential V(r)=Ar -4 +Br -3 +Kr -1 , which express the interactions between ions and atoms.
采用连续分数法得到了表示原子、离子间相互作用势V(r) =Ar-4+Br-3 +Kr-1的Schr dinger方程的精确解 。
2.
By means of the continuous fraction method,an exact solution of the radial Schro¨dinger equation for the potential V(r)=α1r4+α2r+β3r-1+β2r-3+β1r-4is obtained.
采用连续分数法，得到势Ｖ（ｒ）＝α１ｒ４＋α２ｒ＋β３ｒ－１＋β２ｒ－３＋β１ｒ－４的径向Ｓｃｈｒｏ¨ｄｉｎｇｅｒ方程的解析解，并作适当的讨
3.
By means of the continuous fraction method,an exact solution of the radial Schrdinger equation for the potential V(r)=α 1r 10 +α 2r 4+α 3r 2+β 3r -4 +β 2r -6 +β 1r -10 is obtained here.
采用连续分数法，得到势函数Ｖ（ｒ）＝α１ｒ１０＋α２ｒ４＋α３ｒ２＋β３ｒ－４＋β２ｒ－６＋β１ｒ－１０的径向Ｓｃｈｒ¨ｏｄｉｎｇｅｒ方程的精确解。
4) Gauss continued fraction method
Gaus连续分数法
5) SMJ algorithm
多数据流连接算法
6) numerical differential algorithm
数值微分算法
补充资料：连分数
| 连分数 continued fraction 如果a0，a1，a2，…an，…都是整数，则将 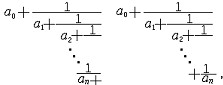 分别称为无限连分数和有限连分数 。可简记为[a0 ，a1，a2，…，an，…]和[a0，a1，a2，…，an]。一般而言 ，一个有限连分数表示一个有理数，一个无限连分数表示一个无理数。也可把连分数推广到a0，a1，a2，…，an，…都是实数的情形，并将上述形式的连分数分别叫无限连分数和有限连分数 。近代数学的计算需要，还可将连分数中的a0，a1 ，a2，…，an，…取成以x为变元的多项式。在近代计算数学中它往往与某些微分方程式差分方程有关，与某些递推关系有关的函数构造的应用相联系。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条