1) Cycloid cam


摆线凸轮
1.
In this paper,models of the cycloid cam mechanism are established.


对摆线凸轮-从动杆机构,提出线性及非线性模型,并应用拉氏变换分析了该系统的动力学问题,为进行现代化设计提供了理论依据。
2) swing link cam


摆杆凸轮
1.
The theoretical contour curve equation and the actual contour curve equation of two sides of swing link cam are deduced in the pole coordinate system respectively, and the equation based on two different pole coordinate system are consolidated into one in succession.
研究了摆杆凸轮左右两部分理论轮廓曲线方程和实际轮廓曲线方程,并把两组极坐标系中的方程统一于一组极坐标系中。
3) rocking cam


摇摆凸轮
4) swing cam


摆动凸轮
1.
By means of chemical composition analysis,hardness testing,fracture analysis and so on,the reason of the fracture of 40Cr swing cam which was applied to load-carrying vehicle was analysed.
采用化学成分分析、硬度测试和断口分析等方法分析了某载重车辆钢摆动凸轮断裂的原因。
6) MFB-Ⅱ cam


复合摆线Ⅱ型凸轮
补充资料:摆线
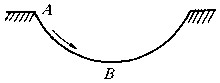
| 摆线 cycloid 一个圆在一条定直线上滚动时,圆周上一个定点的轨迹。又称旋轮线。圆上定点的初始位置为坐标原点,定直线为x轴。当圆滚动j 角以后,圆上定点从 O 点位置到达P点位置。当圆滚动一周,即 j从O变动2π时,动圆上定点描画出摆线的第一拱(图1)。 再向前滚动一周, 动圆上定点描画出第二拱,继续滚动,可得第三拱,第四拱……,所有这些拱的形状都是完全相同的 ,每一拱的拱高为2a(即圆的直径),拱宽为2πa(即圆的周长)。摆线有一个重要性质,即当一物体仅凭重力从A点滑落到不在它正下方的B点时,若沿着A,B间的摆线,滑落所需时间最短(图2),因此摆线又称最速降曲线。
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条