1) Sierpinski fractal dimension
Sierpinski分维数
1.
Based on the fractal concept of Sierpinski carpet the Sierpinski fractal dimension D_s,characterizing the structure of soil pore,is obtained from the measured data,and its v.
基于Sierpinski地毯的分形概念,结合量测数据给出了描述孔隙结构的Sierpinski分维数并研究其差异性。
2) Sierpinski number
Sierpinski数
3) quasi-Sierpinski fractal
准Sierpinski分形
4) Sierpinski three fractal gasket
Sierpinski三分垫
1.
In this paper we find a new method to make Sierpinski three fractal gasket,and we hold the exact value of its Hausdorff dimension and measure.
给出了Sierpinski三分垫的一种新的构造法,并求出了它的Hausdorff维数与测度的精确值。
5) 3-level Sierpinski gasket
三分Sierpinski垫
1.
The Cauchy transform F(z) ofα-Hausdorff measure restricted on 3-level Sierpinski gasket with a=1+1og2/log3,similarly to the case on Sierpinski gasket,presents some unusual geometric behavior.
三分Sierpinski垫上的α(=1+(log_2)/(log_3))维Hausdorff测度的Cauchy变换F(z)和二分的情形一样,表现出一些不平常的几何性质。
2.
Let K be the 3-level Sierpinski gasket with vertices 1, e~(2πi/3),e~(4πi/3);it has Hausdorff dimension α = 1 + log2/log3.
设K为复平面C上的三分Sierpinski垫,顶点分别为1,e~(2πi/3),e~(4πi/3),K的Hausdorff维数α=1+log2/log3。
6) Sierpinski fractal
Sierpinski分形
1.
For the widely studied and used Sierpinski fractal antennas, the analysis procedure using moment methods (MOM) is firstly presented in this paper.
对于Sierpinski分形天线这一当前研究及应用的热点问题,本文首先给出了传统矩量法(MOM)的分析过程。
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 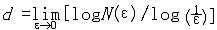 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条