1) Fresnel approximation algorithm
菲涅耳近似再现算法
2) Fresnel approximation
菲涅耳近似
1.
Both results of the theoretical analysis and the computer simulation show that the quality of the images acquired by Fresnel approximation and by angular spectrum method are better than by convolution,and the recon.
根据全息理论和线性系统理论,采用离轴无透镜傅里叶变换全息记录光路,对利用菲涅耳近似法、基于瑞利—索末菲衍射积分的卷积法以及角谱理论方法数值重建全息图进行了比较研究,并做了计算机模拟验证。
2.
when the propagation and transformation of complex amplitude function(CAF)of point light source is dealed with,the Fresnel approximation is usually used withquadratic instead of spherical wavefront in order to simplify the mathematic operationWhen the off-axis angle of point source is large,this approximation is far apart from theexperiment phenomina,and the errors are evident.
通常应用菲涅耳近似，以二次曲面代替球面，但是，当离轴角较大时，菲涅耳近似的误差较大，明显地与实验现象不符。
3) Fresnel-transform reconstruction
菲涅耳变换法再现
1.
Based on analyzing resolution of digital holographic system and sampling space in reconstructed image plane,a simple,convenient and effective method is presented,which can increase the display resolution of the reconstructed field in Fresnel-transform reconstruction of digital holograms.
在分析数字全息系统的最小分辨距离和再现像平面上的采样间隔的基础上,提出了一种在用菲涅耳变换法再现数字全息图时,能清楚显示再现像细节的简单方法,这种方法能有效地提高再现场的显示分辨率。
4) Fresnel approximation integral
菲涅耳近似核hFz
1.
Fresnel approximation integral and Fresnel-Kirchhoff integral kernel of numerical reconstruction in digital holography were analyzed theoretically.
对数字全息再现中的菲涅耳近似核hFz和Fresnel-Kirchhoff衍射积核hz进行了理论分析。
5) Fresnel diffraction approximation
菲涅耳衍射近似
1.
With the Fresnel diffraction approximation method,the influences of the collimated lens and standard lens surface errors on the transparence testing are.
根据菲涅耳衍射近似理论,就菲佐干涉仪中的准直镜和标准镜面形误差对透过检测的影响进行了研究。
6) Fresnel-Kirchhoff approximation
菲涅耳-柯西霍夫近似
补充资料：菲涅耳衍射
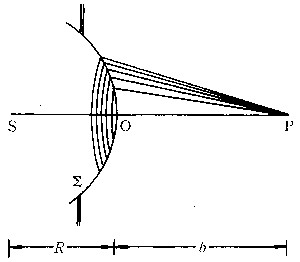
| 菲涅耳衍射 Fresnel diffraction 光源和观察屏离障碍物（孔或屏）为有限远时的衍射 。以单色点光源照射圆孔，在有限远处设置观察屏，在屏上将观察不到圆孔的清晰几何影，而是一组明暗交替的同心圆环状衍射条纹。以不透光的圆屏代替圆孔，在原几何影中心可观察到亮点，外围与圆孔衍射一样是明暗交替的圆环条纹 。以上是菲涅耳衍射的典型例子。根据惠更斯-菲涅耳原理计算菲涅耳衍射的强度分布时，必须对波前作无限分割，然后用积分求次波的合振幅，计算比较复杂。在处理圆孔或圆屏衍射时常用菲涅耳半波带法，它是用较粗糙的分割来代替对波前的无限分割，相应地，次波叠加时的积分可简化成多项式求和。此法虽然不够精确，但可较方便地得出菲涅耳衍射的主要特征。 菲涅耳圆孔衍射 如图1，S是波长为λ的点光源，P为观察点。考虑半径为R的球面波前Σ，它与SP交于O点。以观察点P为中心，依次以 b＋λ／2，b＋λ，b＋3λ／2，b＋2λ，……为半径作一系列球面，把Σ分割成许多以O为心的圆环带。每个环带看成是发射次波的一个单元，相邻两环带所发次波到达P点的光程差（见光程）均为λ／2（对应相位差为π），故每个环带称为半波带。从中心O算起，设第k个半波带在P点引起的振幅为ak，则有akαFΔSk／rk ，式中ΔSk为第k个波带的面积，rk为它到P点的距离，F为该波带处的倾斜因子。从几何上可证ΔSk／rk近似为常数，故ak仅由倾斜因子决定，按菲涅耳的假设，有a1 ＞a2＞a3＞…。故P点的合振幅为A＝a1－a2＋a3－a4 ＋……
若在波前Σ处放置一带圆孔的无穷大不透光屏，圆孔中心在连线SP上，则P点的合振幅A就由未被遮挡的半波带数决定，A等于有限项之和，其大小由露出的半波带数的奇偶性决定。半波带的划分与观察点P的位置有关，当P点沿轴线移动时，露出的半波带数的奇偶性将交替变化，P点的强度也作明暗交替变化。当观察点向轴外移动时，露出的半波带不断变化，强度也相应地作明暗交替变化，于是形成圆环条纹。 菲涅耳圆屏衍射 以不透光的圆屏代替圆孔(图2)，中央部分的半波带将被挡住，设正好挡掉k个半波带，则P点振幅为： A＝ak+1－ak+2＋ak+3－……＋a∞＝ak+1/2 得圆屏衍射图样的中心点为亮点，周围与圆孔衍射一样是明暗交替的同心圆环条纹。1818年，A.-J.菲涅耳参加了法国科学院主办的一次征文竞赛，发表了关于衍射理论的论文。评审委员会成员之一的S.D.泊松反对光的波动说，他仔细审核了菲涅耳的理论，得出圆屏几何影中心应为亮点的结论（故称泊松亮点），他利用这一当时看来与日常经验相违背的结论对菲涅耳的理论提出异议。但过后不久，D.F.J.阿拉戈在实验中果真发现了几何影中心为亮斑（故又称阿拉戈斑）。这成为菲涅耳的衍射理论和光的波动说取得决定性胜利的标志。
菲涅耳波带片 对特定的观察点可设计一种特殊的遮光屏，把所有奇数或偶数的半波带遮掉，则观察点将是强度大大增强的亮点，如同光源的像点一样，这种特殊遮光屏称为菲涅耳波带片，它与透镜一样具有成像性质，其焦距为 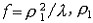 ，ρ1为第一个半波带的半径 ，λ为波长。与透镜不同的是，除上述主焦距外，还有f／3，f／5，f／7，…等次焦距。波带片除有会聚性质外，还有发散性质，即存在－f，－f／3，－f／5，…等一系列虚焦距 。现代波带片的种类很多，除上述振幅型的外，还有相位型；透射率有矩形函数，也有正弦函数；有用于可见光波段，也有用于微波波段，等等。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条