1) variable dimension fractal
变维分形
1.
Newton s second Law, the law of Gravity and the law of Coulomb with the form of variable dimension fractal;
变维分形形式的牛顿第二定律及万有引力定律和库仑定律
2.
This paper solves the forecast problems of various models by using constant dimension fractal, variable dimension fractal and parameter transformation fractal methods.
本文应用常维分形、变维分形及参数变换分形等方法求解不同模型的预测问题。
3.
Because of the inconstant fractal dimensions in practical application,the concept of variable dimension fractal was introduced to predict equipment failure frequencies based on the illustration of fractal theory.
在介绍有关分形理论的基础上,针对实际应用中分形维数不恒定的问题,将变维分形的概念引入到装备故障频数预测中。
2) variable dimension fractals
变维分形
1.
, sectioned variable dimension fractals, this paper discusses the forecast of typhoon tracks.
应用分形分布模型n=C/r~D的推广形式,即分段变维分形预测台风路径,方法简便易行。
2.
Hong-Yang spectrum which coincides better with the measured spectral values are analyzed with the variable dimension fractals (the fractal dimension D is the function of characteristic scale r instead of a constant).
用变维分形方法（分维数是特征线度的函数,而不是常量）分析了与实测谱值符合良好的Hong—Yang谱,根据分析结果讨论了用分形方法对实测谱值的拟合与插值,效果很好。
3.
This paper decides the coast line length by using variable dimension fractals (fractal dimension D is the function of characteristic scale r instead of a constant).
应用变维分形(即分维数D是特征线度r的函数,而非常数)来确定海岸线的长度。
3) constant dimension fractal and variable dimension fractal
常维分形和变维分形
4) sectioned variable dimension fractals
分段变维分形
1.
, sectioned variable dimension fractals, this paper discusses the forecast of typhoon tracks.
应用分形分布模型n=C/r~D的推广形式,即分段变维分形预测台风路径,方法简便易行。
5) variable dimension fraction
连续变维分形
6) fractal time-varying dimension
分形时变维数
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 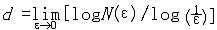 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条