1) local fractal dimension
局部分形维数
1.
Hursts rescaled range (R/S) analysis and Wolfs attractor reconstruction technique have been adopted to estimate the local fractal dimensions and the local largest Lyapunov exponents in terms of the time series pressure fluctuations obtained from a gas liquid solid three phase self aspirated reversed flow jet loop reactor,respectively.
应用重标度范围（Ｒ／Ｓ）分析技术和吸引子重构技术，初步研究了下喷自吸环流反应器内气－液－固三相流动的时序压力波动的局部分形维数和局部最大Ｌｙａｐｕｎｏｖ指数特性。
2) local fractals
局部分形维
1.
A novel method of structural irregularity measurements,as a key diagnostic factor,was given and boundary asymmetry measurements using local fractals were presented as well.
针对计算机辅助早期诊断黑色素瘤中皮肤肿瘤轮廓的结构不规则性和不对称性检测问题,本研究提出了多尺度局部分形维算法。
3) local fractalscale
局部分形指数
4) local dimension
局部维数
1.
The paper discusses the local dimension of self-similar set caused by a family of contracted mappings satisfying open set condition on R d
讨论了 Rd上满足开集条件的一族压缩映射所生成的自相似集的局部维
2.
The paper discusses the local dimension of invariant set caused by a family of contracted mappings on R 1 which satisfy the open set condition.
讨论了 R1 上满足开集条件的一族压缩映射所生成的自相似集的局部维
3.
This paper puts forward the concept of local dimension, and, based on the extension of Hausdorff dimension, derives the relationship between local information dimension, local stuff dimension and dimension n , possibility density.
提出了局部维数的概念，并在对Ｈａｕｓｄｏｒｆ维数推广的基础上推导出局部信息维数及局部填充维数与维数ｎ及概率密度的关系，进而推导出了经典分形场的动力学方程及量子体系分形场方程，从而有效地诠释了一些自然现象及生物现象中存在自相似结构的动力学机制。
5) local fractal
局部分维
1.
But it is proved in practice that the cartographic point group usually shows nonuniformity of local fractal characteristics.
本文在分维扩展方法的基础上,提出了一种基于滑动窗口的局部分维分析方法——元分维模型,并通过实践证明该方法可以有效地揭示地图点群空间分布特征的差异,从而为地图点群目标的空间分布特征分析提供了一个新的思路。
6) Local fuzzy fractal dimension
局部模糊分形维度
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 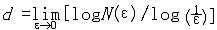 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条