1) Hamilton canonical equation
Hamilton正则方程
1.
The semi-analytical solution for Hamilton canonical equation is employed widely in the engineering problems in recent years.
近年来,Hamilton正则方程半解析法在工程问题上的应用越来越广泛,但至今未见有关这种方法收敛性和对称性问题研究的文献。
2.
In terms of the generalized Hamilton variation principle,the non-homogeneous Hamilton canonical equation for piezothermoelastic bodies was derived.
根据广义的Hamilton变分原理推导出了压电热弹性体非齐次的Hamilton正则方程。
3.
Based on the semi-analytical solution for Hamilton canonical equation,the linear equation of each layer is established separately.
将厚度不连续梁板视为层合板,分别应用Hamilton正则方程半解析法建立每一层的线性方程。
2) regular Hamiltonian equation
Hamilton正则方程组
3) homogeneous Hamilton canonical equation
齐次Hamilton正则方程
4) higher order Hamilton's canonical equations
高阶Hamilton正则方程
5) Hamiltonian canonical equations
Hamilton系统正则方程
6) no-homogeneous Hamilton canonical equation
非齐次Hamilton正则方程
补充资料：正则方程
| 正则方程 canonical equations 用广义坐标qi和广义动量pi（i＝1，2，…，N）联合表示 受理想约束的完整保守系统的力学方程。又称哈密顿方程。可写为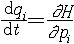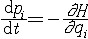：  ， （i＝1，2，…，N）式中H＝T2－T0＋V为哈密顿函数，T2和T0分别为动能T中用广义动量表示的二次齐次式和零次齐次式(即不含pi，仅含qi和t之式)，V为用广义坐标表示的势函数，对于定常系统（约束方程不包含时间t）T0＝0，T＝T2，则H＝T＋V，即这种力学系统的哈密顿函数就是这系统用广义动量和广义坐标表示的机械能。正则方程是2N个一阶微分方程组，其形式上的优点是每一式只有一个导数，且都在等号左边，右边是q，p，t的函数。若令 q1＝x1，p2＝x2…，qN＝xN，p1＝xN+1，p2＝xN +2…，pN＝x2N，则正则方程可写成：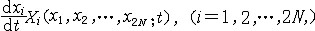
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |