1) elasticity
[英][,i:læ'stɪsəti] [美]['ilæ'stɪsətɪ]


弹性力学
1.
Utilize differential equation to find out the solutions of plane problems in elasticity;


利用微分方程求解弹性力学平面问题
2.
Boundary contour method based on the eqvivalent BIE of two dimensional linear elasticity;
弹性力学平面问题的等价边界积分方程的边界轮廓法
3.
Reproducing kernel particle method with complex variables for elasticity;


弹性力学的复变量重构核粒子法
2) Elastic mechanics


弹性力学
1.
Elastic Mechanics Analysis of Prestressing Force in Round Structure Caused by Manufacture Discrepancy;
环形结构制作误差引起的预应力弹性力学解
2.
Memory law of radial coordinates formula of elastic mechanics;


弹性力学极坐标公式的记忆规律
3.
Study of the elastic mechanics problem in narrow rectanglar girder by the singularity function;
狭矩形截面梁弹性力学问题的奇异函数法研究
3) elasticity mechanics


弹性力学
1.
Discussion of elasticity mechanics properties of elbow rod fitting model for injection molding machine (part two)
注塑机肘杆合模机构弹性力学性能的探讨(二)
2.
Discussion of elasticity mechanics properties of elbow rod fitting model for injection molding machine (part one)
注塑机肘杆合模机构弹性力学性能的探讨(一)
3.
Based on the correlative theory of elasticity mechanics,a mathematical analytical model on constant-tensility ropeway system was established for the derivation of the movement equations of the ropeway.
根据小型船艇海上补给的特点,提出了一套纵向锚泊补给的海上补给方式及补给装置,利用弹性力学的有关理论,建立补给装置恒张力索道系统数学分析模型,推导索道运动方程。
4) theory of elasticity


弹性力学
1.
Cellular automata for analysis of plane problems in theory of elasticity;


平面弹性力学中的细胞自动机方法
2.
While Hamiltonian system was led to solution of elastic theory a new systematic methodology for theory of elasticity was established and a symplectic orthogonality relationship was presented (Zhong Wanxie, 1995).
利用平面弹性与板弯曲的相似性理论,将弹性力学新正交关系中构造对偶向量的思路推广到各向同性薄板弹性弯曲问题,由混合变量求解法直接得到对偶微分方程并推导了对应的变分原理。
3.
In a new systematic methodology for theory of elasticity a new dual differential matrix is presented by changing the order of the dual vectors in reference and a new orthogonality relationship is found and proved for isotropic problems of three-dimensional theory of elasticity.
在弹性力学求解新体系中 ,将文献 [3]对偶向量进行重新排序后 ,提出了一种新的对偶微分矩阵L ,对于各向同性 3维弹性力学问题发现了一种新的正交关系 。
5) mechanics of elasticity


弹性力学
1.
The method of sum function to solve plane problem of mechanics of elasticity has also been complemented,and the area of practicle problem to be solved by means of mechanics of elasticity has .
采用应变和函数法对该问题进行了详细的级数解答,与变分法结果进行比较,证明了该方法的正确性和适用性,完善了用和函数求解平面弹性力学问题的方法,扩大了弹性力学解决工程实际问题的范围。
2.
By expressing the non-continuous loads of a plane problem in the mechanics of elasticity in terms of derivate or integral of δ function and expanding them into Fourier series,such loads can be transformered into continuous surface forces a long the whole boundary, that much simplify the solution of the boundary conditions and the problem itself.
将弹性力学平面问题中的不连续荷载表为δ函数、δ函数的导数或积分,并展成Fourier级数,从而使其变换成沿整个边界上的连续分布的面力,大大简化了问题的边值条件和问题的求解。
3.
In this paper the importance of stress positive-negative regularity on tilt section in plane problem of mechanics of elasticity is introduced and the regularity is proved.
介绍了弹性力学平面问题中斜截面上应力的正负规定的重要性及其对该规定的论证;并举例说明了该规定在实际问题中的应用。
6) elasticity
[英][,i:læ'stɪsəti] [美]['ilæ'stɪsətɪ]


弹性;弹力;弹性力学
补充资料:弹性力学
| 弹性力学 elasticity 研究弹性物体在外力和其他外界因素作用下产生的变形和内力的固体力学分支。又称弹性理论。它是材料力学、结构力学、塑性力学和某些交叉学科的基础,广泛应用于建筑、机械、化工、航空、航天等工程领域。 简史 中国的郑玄是最早定量地研究弹性定律的人。英国的 R.胡克于1678年和法国的 E.马略特于 1680年分别独立地提出了弹性体的变形和所受外力成正比的定律,后被称为胡克定律。I.牛顿于1687年确立了力学三定律(见牛顿运动定律),同时数学也在飞跃发展,建立弹性力学数学理论的条件已大体具备。17世纪末,人们开始研究梁的理论。到19世纪20年代法国的 C.-L.-M.-H.纳维和 A.-L.柯西才基本上建立了弹性力学的数学理论 。柯西在 1822~1828年发表的一系列论文中,明确地提出了应变、应变分量、应力和应力分量的概念,建立了弹性力学的几何方程、运动(平衡)方程、各向同性以及各向异性材料的广义胡克定律,从而奠定了弹性力学的理论基础 。1855~1856 年间法国的A.J.C.B.de圣维南发表了柱体扭转和弯曲的论文,其中理论结果和实验结果密切吻合,为弹性力学的正确性提供了有力的证据 。1881年德国的H.R.赫兹解出了两弹性体局部接触时弹性体内的应力分布。1898年德国的G.基尔施在计算圆孔附近的应力分布时,发现了应力集中。这些成就解释了过去无法解释的实验现象,对提高机械、结构等零件的设计水平起了重要作用。在这个时期,弹性力学的一般理论也有很大发展,建立了各种关于能量的定理和原理,如弹性力学虚功原理和弹性力学最小势能原理 ,1872年意大利的 E.贝蒂建立的功的互等定理 ,1873~1879年意大利的 A.卡斯蒂利亚诺建立的弹性力学最小余能(即余应变能)原理。还发展了许多有效的近似计算、数值计算和其他计算方法 ,如瑞利-里兹法,为直接求解泛函极值问题开辟了道路,推动了力学、物理、工程中近似计算的发展 。1913~1915 年俄国的布勃诺夫和伽辽金提出了布勃诺夫-伽辽金法 。后来 ,苏联的穆斯赫利什维利于20世纪 30年代发展了复变函数的应用 ,为求解弹性力学平面问题提供了有力的工具。积分变换和积分方程等在弹性力学中的应用也有了新发展。从20世纪20年代起,弹性力学在发展中出现了许多边缘分支:各向异性和非均匀体理论,非线性板壳理论和非线性弹性力学,热弹性力学,气动弹性力学,水弹性力学和粘弹性力学等。磁弹性和微结构弹性理论也开始建立起来。此外还建立了弹性力学广义变分原理。 基本规律 包括变形连续规律 、应力-应变关系和运动(或平衡)规律 。弹性力学许多定理 、公式和结论都可从这3个基本规律推导出来。 ①变形连续规律。弹性力学只限于考虑原来连续、变形后仍为连续的物体,在变形过程中,物体不产生新的不连续面。如果物体中本来就有裂纹,则只考虑裂纹不扩展的情况。反映变形连续规律的数学方程有两类:几何方程和位移边界条件。 ②应力-应变关系 。弹性体中一点的应力状态和应变状态之间存在着一定的联系,应力和应变之间存在着对应的关系。若应力和应变呈线性关系,这个关系便称为广义胡克定律(见胡克定律)。 ③运动(或平衡)规律。处于运动(或平衡)状态的物体,其中任一部分都遵守牛顿运动定律。反映这个规律的数学方程有两类:运动微分方程和载荷边界条件。 弹性力学问题的提法和求解 为了阐明一个弹性力学问题,需要说明物体的形状和物体各部分由什么材料组成;说明物体所承受的载荷,包括体积力fi ,自由边界上的载荷 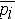 ;说明此物体和其他物体的连接情况。对弹性力学的平衡问题,说明上述3个方面即可 。但对弹性力学的动力问题 ,还需说明物体的初始状态。 ;说明此物体和其他物体的连接情况。对弹性力学的平衡问题,说明上述3个方面即可 。但对弹性力学的动力问题 ,还需说明物体的初始状态。求解一个弹性力学问题,就是设法确定弹性体中各点的位移、应变和应力共15个函数。但在各种具体问题中,常常只关心其中的某几个函数。所以在实用上,往往不必确定全部函数。求解时可用实验方法、数学方法,也可用实验和数学相结合的方法。实验方法是用机械的、电的、光的以及其他手段在实物上或模型上测量所需的量。许多复杂而难于计算的问题都是用实验方法求解的(见实验应力分析)。数学方法就是根据几何方程 、应力-应变关系 、运动(或平衡)微分方程、位移和载荷边界条件以及初始条件,解出ui、εij、σij等 15个函数 。数学方法的优点是提供的数据比较全面 ,但只适用于不太复杂的问题。对于一些实用上重要的弹性力学问题,常需同时用实验和数学两种方法求解,以保证结论的可靠性。 常用的数学方法 可分成两类: ①精确解法。包括分离变量法和复变函数法。弹性力学中的许多精确解是用分离变量法求得的。根据物体的形状 ,选择一合适的曲线坐标系并写出相应于该坐标系的弹性力学微分方程和边界条件,如果微分方程中的变量能够分离,通常便可求得问题的解。能用分离变量法求得精确解的问题有:无限和半无限体的问题,球体和球壳的问题,椭球腔的问题,圆柱和圆盘的问题等。能化为平面调和函数或平面双调和函数的问题,它们当中的许多重要精确解都是用复变函数法求得的。 ②近似解法。为求解一些复杂问题,在弹性力学中还发展了许多近似解法。能量法就是其中用得最多的一类方法 ,它把弹性力学问题化为数学中的变分问题(泛函的极值和驻值问题) ,然后再用瑞利-里兹法求近似解 。工程界当前广泛使用的有限元法是能量法的一种新发展。差分法也是一种常用的近似解法,其要点是用差商近似地代替微商,从而把原有的微分方程近似地化为代数方程。此外,边界积分方程、边界元法和加权残数法对解某些问题也是有效的手段。 工程结构元件的实用理论 从广义上说 ,各种工程结构元件(如杆、板、壳)的实用理论都是弹性力学最有实用价值的分支。这些实用理论分别依据结构元件形状及其受力的特点,对位移分布作一些合理的简化假设,对广义胡克定律也作相应的简化,从而使数学方程既得到充分简化又保留了主要的力学特征。从弹性力学看,这些结构元件的实用理论都是近似理论,其近似性大多表现为按照这些理论计算得到的应力和应变不能严格满足胡克定律。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条