1) volume fractal dimension
体积分形维数
1.
Pore volume fractal dimensions of fly ash - cement paste at different ages and its pore volume fractal dimensions were determined by MIP(mercury intrusion porosimetry) on experiments.
采用压汞法对不同龄期粉煤灰-水泥浆体的孔分形结构进行了实验研究,测定了复合浆体孔体积分形维数,探讨了孔体积分形维数与孔隙率,孔表面积、平均孔径、孔分布及宏观力学性能的关系。
2.
The relationship of pore volume fractal dimension with porosity,pore area,pore size distribution and phosphate slag content are investigated.
研究表明,磷渣-水泥浆体的孔结构具有明显的分形特征,孔体积分形维数在2。
2) pore volume fractal dimention
孔体积分形维数
1.
Porous nickel\'s pore volume fractal dimention is determined by data of MIP based on Menger-sponge model,pore structures of porous nickel is found to have typical fractal nature and the values of fractal dimension are between 2.
用压汞法对用粉末冶金法制备的多孔镍试件进行了测试,得到了多孔镍试件的孔隙率及孔径分布曲线,并以Menger海绵体模型为基础,根据压汞实验数据确定了多孔镍试件的孔体积分形维数,发现多孔镍的孔隙结构具有明显的分形特征,分形维数在2。
3) steel fiber content
钢纤维体积分数
4) fiber volume fraction
纤维体积分数
1.
Effect of fiber volume fraction on friction and wear properties of C/C composites;
纤维体积分数对炭/炭复合材料摩擦磨损性能的影响
2.
Calculation of fiber volume fraction for multidirectional filament wound glass-fiber/epoxy tubes;
多向纤维缠绕玻璃钢管的纤维体积分数
3.
The relationships of the loop length, stitch density and thickness of fabrics to yarn linear density were analyzed with the experiment data, and the fiber volume fraction of glass fiber plain knitted fabrics was estimated theoretically.
通过对针织物结构参数的研究,分析了玻璃纤维针织物线圈长度、密度以及厚度与纱线线密度的关系,并从理论上推导了纬平针织物的纤维体积分数。
5) fibre volume fraction
纤维体积分数
1.
Effects of various fibre volume fraction on the performances of C/C composite;
纤维体积分数对炭/炭复合材料性能的影响
2.
In this paper, the effects of the fibre volume fraction on mechanical properties of K 3D/MCPA composites are presented.
本文研究了纤维体积分数对三维编织芳纶纤维增强铸性尼龙 (简称K3D MCPA)复合材料力学性能的影响。
6) fiber volume content
纤维体积分数
1.
Based on three group of integer felts with different fiber volume content were densified with CVD pyrolytic carbon, and a model of gas transport within a integer felt on the course of CVD process, the effect of carbon fiber volume content on the densification course of CVD (chemical vapor deposition) was investigated.
将3组不同纤维体积分数的整体毡采用等温CVD进行沉积热解炭增密,结合CVD沉积过程中整体毡内气体传质数学模型,研究了整体毡的纤维体积分数对CVD增密过程的影响,研究结果表明:纤维体积低的整体毡沉积时增重率高;纤维体积分数高的整体毡容易获得较高密度的C/C复合材料;纤维体积分数超过35％的整体毡经过300 h的化学气相沉积,坯体的体积密度能达到1。
2.
The geometry model formular is used to deduce the length of yarns,the oridentation angle of the nodulated yarns and the fiber volume content on some typical 2.
借助模型推导出纱线在几种典型结构(浅交弯联、浅交直联、深角联)的单元体结构内的纱线长度、接结经的取向角和纤维体积分数,并对材料进行拉伸、压缩性能预测。
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 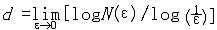 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条