1) half variation function


半变差函数
1.
Structural analysis of half variation function of coal thickness;


煤厚半变差函数的结构分析
2) variation function


变差函数
1.
Recent years,variation function is becoming more important when we research reservoir heterogeneity.
近年来,变差函数在储层非均质性研究中起到很大作用。
2.
All kinds of data can be integrated by variation function.


通过使用变差函数,将地质、露头、三维地震、测井等静态和生产动态等各种信息有机地综合在一起,提高了井间砂体预测的精度,对于预测相似条件下稀井网地区的储集层分布也有理论指导意义。
3.
To improve the quality of the restored images,a variation function as part of regularization penalty term was introduced to the reconstruction algorithm of EIT.
为提高电阻抗静态重构图像的质量,研究将离散变差函数引入到重构算法中,形成混合正则化重构算法,并对计及颅骨的颅内异物进行了重构成像。
3) Variogram function


变差函数
1.
Multiscale edge detection based on image variogram function;


基于图像变差函数的多尺度边缘检测
2.
New multiscale edge detection method for noise image based on variogram function;


基于变差函数的噪声图像的多尺度边缘检测
3.
This paper proposes a novel algorithm for segmentation of texture image based on variogram function.
本文基于变差函数提出一种图像纹理分割的新方法 。
4) variogram
['vɛəriə,ɡræm]


变差函数
1.
The acquirement of robust variogram in reservoir modeling;


储层建模稳健变差函数的求取
2.
Application of variogram to automatic identification of sedimentary microfacies;


变差函数在沉积微相自动识别中的应用
3.
Sensitivity of variogram in stochastic modeling;


随机建模中变差函数的敏感性研究
5) variation of function


函数变差
6) Semivariance


半方差函数
1.
The result of semivariance analysis showed that the metal concentrations were correlated in .
通过半方差函数分析,发现10种重金属元素在一定范围内均存在空间相关性。
2.
Based on gridding sampling,soil water was conducted with Trime measuring system in pear orchard of Yantai Academy of Agricultural Sciences from April to August in 2005,and the soil water statistic characteristic,semivariance,fractal dimension and the law of temporal and spatial distribution were also studied.
2005年4~8月期间,利用Trime水分速测系统,采用网格化取样方式对烟台农科院梨园的土壤(0~30cm)水分的90个样点进行了四次取样,并运用传统统计学和地统计学方法对土壤水分的数据统计特征、半方差函数和分维数及其时空分布规律进行了分析。
补充资料:有界变差函数
| 有界变差函数 bounded variation,function of 定义在区间[a,b]上,并能表为两个单调增函数之差的实值函数。属常用的函数类,它有许多好的性质,例如:有界变差函数必为有界函数;两个有界变差函数的和、差、积仍为有界变差函数;有界变差函数在[a,b]上黎曼可积;有界变差函数在[a,b]上几乎处处可导,导函数在[a,b]上勒贝格可积。此外还有,平面上由y=f(x)表示的曲线C可求长的充分必要条件是f为有界变差函数。应注意的是,连续函数不一定为有界变差函数。例如: 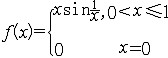 。 。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条