1) dynamic network flow


动态网络流
1.
Dividing the aggregate network volume into connections between host-pairs, we get a connection-oriented model in micro perspective—the dynamic network flow model.
动态网络流模型在微观层面上通过对流量的细分,建立了网络上主机之间的数据交互模型。
2.
In addition,based on dynamic network flow theory,a time-route assignment model with flight level decision parameters for short-term area traffic flow management is proposed to meet the need of Chinese air traffic flow management(ATFM) work.
对管制区短期流量管理问题进行了研究,针对现有模型在约束条件和控制方法中的不足,不仅首次引入了流量控制事件的概念和相应的约束条件,而且在使用动态网络流理论建立了管制区短期空中交通流量管理模型过程中,还新增加了飞行高度层这一决策变量,使本文提出的时隙-航线分配模型与中国管制工作实际更加吻合。
2) pseudo dynamic network current


伪动态网络流
1.
An urban power network(UPN) optimizing approach is presented,based on the theory of pseudo dynamic network current(PNC).
提出了一种基于伪动态网络流的城网优化算法 ,建立了相应的网络模型 ,采用了修正费用伪动态网络流算法。
3) dynamic network


动态网络
1.
Building the Dynamic Network of Mass Customization;


大规模定制生产线的动态网络构造与仿真
2.
Improved Ant Colony Algorithms to the Shortest Path Problem in Dynamic Networks;


动态网络中最优路径问题的改进蚁群算法
3.
Particle swarm optimization for open vehicle routing problem in dynamic network


开放式动态网络车辆路径问题的粒子群算法
4) Dynamic Networks


动态网络
1.
Vehicle Routing Problem in Dynamic Networks:Research Status and Prospect;


动态网络车辆路径问题:研究现状及展望
2.
Research on Vehicle Routing Problem with Dynamic Networks;


动态网络车辆路径问题研究
3.
Especially, we develop a shortest path raytracing method with dynamic networks based on the shortest path algorithm.
特别介绍了作者在最短路径算法基础上 ,提出的动态网络最短路径地震射线追踪方法 。
5) trend network


流动网络
1.
In the paper, the methods of both minimum distance and maximum tree derivation are used to classify the trend networks of overseas tourists to the main tourist cities in China, and make correlative study of their clusters.
本文使用最小距离聚类法和最大树模糊聚类法对中国主要旅游热点城市海外旅游流的流动网络进行了分类 ,做了结点间的相关性分析。
6) Dynamic network traffic flow assignment


动态网络交通配流
补充资料:网络流
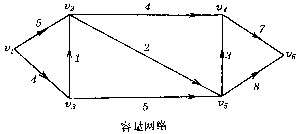
| 网络流 network flows 图论中的一种理论与方法,研究网络上的一类最优化问题。1955年,T.E.哈里斯在研究铁路最大通量时首先提出在一个给定的网络上寻求两点间最大运输量的问题。1956年,L.R.福特和D.R.富尔克森等人给出了解决这类问题的算法,从而建立了网络流理论。所谓网络或容量网络指的是一个连通的赋权有向图D=(V、E、C),其中V是该图的顶点集,E是有向边(即弧)集,C是弧上的容量。此外顶点集中包括一个起点和一个终点。网络上的流就是由起点流向终点的可行流,这是定义在网络上的非负函数,它一方面受到容量的限制,另一方面除去起点和终点以外,在所有中途点要求保持流入量和流出量是平衡的。如果把下图看作一个公路网,顶点v1…v6表示6座城镇,每条边上的权数表示两城镇间的公路长度。现在要问:若从起点v1将物资运送到终点v6去,应选择那条路线才能使总运输距离最短这样一类问题称为最短路问题。如果把上图看作一个输油管道网,v1表示发送点,v6表示接收点,其他点表示中转站,各边的权数表示该段管道的最大输送量。现在要问怎样安排输油线路才能使从v1到v6的总运输量为最大这样的问题称为最大流问题。
最大流理论是由福特和富尔克森于1956年创立的,他们指出最大流的流值等于最小割(截集)的容量这个重要的事实,并根据这一原理设计了用标号法求最大流的方法,后来又有人加以改进,使得求解最大流的方法更加丰富和完善。最大流问题的研究密切了图论和运筹学,特别是与线性规划的联系,开辟了图论应用的新途径。 最大流问题仅注意网络流的流通能力,没有考虑流通的费用。实际上费用因素是很重要的。例如在交通运输问题中,往往要求在完成运输任务的前提下,寻求一个使总运输费用最省的运输方案,这就是最小费用流问题。如果只考虑单位货物的运输费用,那么这个问题就变成最短路问题。由此可见,最短路问题是最小费用流问题的基础。现已有一系列求最短路的成功方法。最小费用流(或最小费用最大流)问题,可以交替使用求解最大流和最短路两种方法,通过迭代得到解决。 目前网络流的理论和应用在不断发展,出现了具有增益的流、多终端流、多商品流以及网络流的分解与合成等新课题。网络流的应用已遍及通讯、运输、电力、工程规划、任务分派、设备更新以及计算机辅助设计等众多领域。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条