1) textural fractal dimension
织构分维数
1.
The textural fractal dimensions and dimensionless length of the slag-metal boundary are calculated from the mixing images under various b.
应用分形理论对其边界的织构分维数及无量纲长度进行了计算。
2) texture volume fraction
织构体积分数
1.
The relationship between the texture volume fractions and rolling true strain can be quantified by the Avrami type equations.
采用X射线衍射测量了1100铝合金不同变形量的冷轧织构,建立了织构体积分数和轧制真应变的数学关系式。
3) microstructure fractal dimension
微结构分形维数
4) structure fractal dimension
结构分形维数
1.
In order to simulate soil spatial structure change and to exactly calculate soil final compaction state when soil grains are compacted,fractal theory is adopted to establish a functional relationship between the particle size distribution,the soil spatial microstructure and the soil compacted deformation parameters,and a soil structure fractal dimension calculation formula is given.
为了准确地模拟土体颗粒在压实过程中空间结构的变化,计算土体压实所能达到的最终状密实态,文章采用分形几何原理,建立了土粒径分布、颗粒空间结构与土体变形参数之间的函数关系,提出了土体空间结构分形维数计算公式,计算分析了土体孔隙通道分形维数值;分析表明,随着压实进行孔隙通道的曲折程度增大,孔隙通道的长度变短,土体密实增加;通过Gaudin-Schuhmann粒度分布方程可以定量地由粒径的分布来判断压实所能达到的终极状态,从而更清晰地分析土体微观结构与压实性能之间关系。
5) fabric structure
纤维织构
1.
The effects of different fabric structure on mechanical properties and microstructure of Cf/SiC composites were investigated.
以先驱体浸渍裂解工艺制备了Cf/SiC复合材料,在相同工艺条件下,研究了四种纤维织构:2。
6) fiber texture
纤维织构
1.
A Method for quantitative fiber texture analysis on the inverse pole figure of hexagonal system materials is developed and the corresponding algorithm program is compiled.
发展出一适于六方系多晶材料反极图上纤维织构定量的方法;编制了相应的计算软件。
2.
A method for quantitative fiber texture analysis on the inverse pole figure of cubic system materials is developed and the corresponding algorithm program is compiled.
发展出一适于立方系多晶材料反极图上纤维织构定量的方法;编制了相应的计算软件。
3.
The elastic constants of TiN thin films with the isotropic and ideal fiber texture were calculated by the Voigt, Reuss and Hill models.
用Voigt、Reuss和Hill模型计算了各向同性和具有理想纤维织构的氮化钛 (TiN)薄膜的弹性常数矩阵 ,计算表明 :材料的弹性矩阵强烈地依赖于材料的织构 。
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 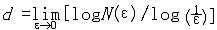 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条