1) helium atom


氦原子
1.
The study of the effect of helium atom on hydrogen molecule by molecular intrinsic characteristic contour theory;
应用MICC理论研究氦原子对氢分子特征轮廓的影响
2.
The variation calculation for the energy of helium atom s 1s3p configuration;


氦原子1s3p组态能量的变分计算
3.
Stark effect on the 1s2s configuration of helium atom;


氦原子1s2s组态的斯塔克效应
2) Helium
[英]['hi:liəm] [美]['hilɪəm]


氦原子
1.
Radiative spectra of helium doubly-excited states;


氦原子双电子激发态的辐射光谱
2.
Calculation of helium ~1D—~3D term intervals for 1snd(n=4—11) states;


氦原子1snd(n=4—11)组态下~1D—~3D谱项分裂值的计算
3.
Absolute generalized oscillator strength measurement of electronic excitations of Helium;


氦原子电子激发跃迁的绝对广义振子强度测量
3) helium-like atom


类氦原子
1.
Variational numerical study of the energy levels for the ground states of helium-like atom systems;
类氦原子体系基态能量的变分法数值研究
4) cluster containing helium


含氦原子簇
5) neutral He atom


中性氦原子
1.
In this paper, the spin state of neutral He atom is discussed in detail with two different methods.
通过两种方法对中性氦原子的自旋态作了详细的讨论 ,尤其是矩阵相乘法的提出和应用 ,能够加深对自旋态物理图像的理
6) the atom He in its ground


基态氦原子
补充资料:液态氦
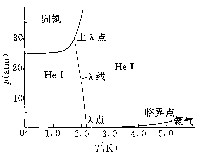
| 液态氦 liquid helium 在极低温度下气态氦转变为液态氦 。由于氦原子间的相互作用(范德瓦耳斯力)和原子质量都很小,很难液化,更难凝固 。富同位素4He的气液相变曲线如图1。4He的临界温度和临界压强分别为5.20K和2.26大气压,一个大气压下的温度为4.215K 。在常压下,温度从临界温度下降至绝对零度时,氦始终保持为液态,不会凝固,只有在大于25大气压时才出现固态。普通液氦是一种很易流动的无色液体,其表面张力极小,折射率和气体差不多,因而不易看到它。液态4He包括性质不同的两个相 ,分别称为HeⅠ和HeⅡ,在两个相之间的转变温度处,液氦的密度、电容率和比热容均呈现反常的增大。两个液相HeⅠ和HeⅡ间的转变温度称为λ点,饱和蒸气压下的λ点为2.172K,压强增加时,λ点移向较低的温度,两个液相的相变曲线为一直线,称为λ线(图1)。
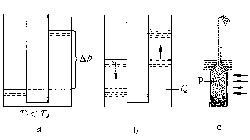
液氦具有一系列引人注目的特点,主要表现在以下几方面。 超流动性 普通液体的粘滞度随温度的下降而增高,与此不同,HeⅠ的粘滞度在温度下降到2.6K左右时 ,几乎与温度无关 ,其数值约为3×10-6帕秒,比普通液体的粘滞度小得多。在2.6K以下,HeⅠ的粘滞度随温度的降低而迅速下降。HeⅡ的粘滞度在λ点以下的温度时立刻降至非常小的值(<10-12帕秒),这种几乎没有粘滞性的特性称为超流动性。用粗细不同的毛细管做实验时,发现流管愈细,超流动性就愈明显,在直径小于10-5厘米的流管中,流速与压强差和流管长度几乎无关,而仅取决于温度,流动时不损耗动能。 对HeⅡ性质的理论研究首先由F.伦敦作出。4He原子是自旋为整数的玻色子,伦敦把HeⅡ看成是由玻色子组成的玻色气体,遵守玻色统计规律,玻色统计允许不同粒子处于同一量子态中。伦敦证明了存在一个临界温度Tc,当温度低于Tc时,一些粒子会同时处于零点振动能状态(即基态),称为凝聚,温度愈低,凝聚到零点振动能状态的粒子数就愈多,在绝对零度时,全部粒子都凝聚到零点振动能状态,以上现象称为玻色-爱因斯坦凝聚 。L.蒂萨认为HeⅡ的超流动性起因于玻色-爱因斯坦凝聚 。由于已凝聚到基态的HeⅡ原子具有最低的零点振动能,故有极大的平均自由程,能够几乎无阻碍地通过极细的毛细管。蒂萨首先提出二流体型,后来L.D.朗道修正和补充了此模型。二流体模型认为HeⅡ由两部分独立的、可互相渗透的流体组成,一种是处于基态的凝聚部分,熵等于零,无粘滞性,是超流体;另一种是处于激发态(未凝聚)的正常流体,熵不等于零,有粘滞性。两种流体的密度之和等于HeⅡ的总密度,温度降至λ点时,正常流体开始部分地转变为超流体,温度愈低,超流体的密度愈大,而正常流体的密度则愈小,在绝对零度时,所有原子都处于凝聚状态,全部流体均为超流体。利用这个二流体模型可解释关于液氦的许多力学和热学性质。 热传导 HeⅠ具有普通流体的导热率,因而当减小压强时,液氦出现激烈的沸腾现象。HeⅡ的导热率要比HeⅠ高出106倍,比铜高出104倍。当温度越过λ点,HeⅠ转变为HeⅡ时,液氦从很坏的热导体突然变为到目前为止最好的热导体。由于HeⅡ的导热率异乎寻常地高,其内部不可能出现温差 ,因而内部不可能汽化,即不能沸腾。当利用抽气方法减低蒸气压时,开始阶段出现激烈的沸腾,温度降低至λ点以下时,HeⅠ转变为HeⅡ,沸腾突然停止,液面平静如镜,汽化只发生在液面。正常流体的导热率与温度梯度无关,纯粹是反映物质性质的量,但HeⅡ的导热率却与温度梯度甚至容器的几何形状有关。 氦膜 任何与HeⅡ接触的器壁上覆盖一层液膜,液膜中只包含无粘滞性的超流体成分,称为氦膜。氦膜的存在使液氦能沿器壁向尽可能低的位置移动。将空的烧杯部分地浸于HeⅡ中时,烧杯外的液氦将沿烧杯外壁爬上杯口,并进入杯内,直至杯内和杯外液面持平。反之,将盛有液氦的烧杯提出液氦面时,杯内液氦将沿器壁不断转移到杯外并滴下。液氦的这种转移的速率与液面高度差、路程长短和障壁高度无关。 热效应 包括机-热和热-机两种效应。如图2a,盛有液氦的两个容器用极细的毛细管C连通,注入液氦,温度低于λ点,右侧液面高于左侧 ,形成压强差Δp。液氦中低熵超流成分能从右侧通过毛细管转移到左侧,而高熵的正常成分不能通过毛细管。这导致右侧液氦的熵增加,左侧的熵减少,这意味着右侧温度升高而左侧温度降低。这种由机械力引起的热量迁移称为机-热效应 。机-热效应的逆过程称为热-机效应,如图2b所示。右侧液氦受热后(吸热Q),低熵的超流成分减少,左侧液氦中的超流成分通过毛细管流向右侧,而正常成分不能通过毛细管,这导致右侧液面升高形成压强差。图2c是演示热-机效应的“喷泉”装置。带毛细管喷嘴的无底玻璃管的填充金刚砂粉末P,用棉花C塞住底部,浸入液氦中。用光照射玻璃管,使管内的液氦温度升高,超流成分激发成正常成分。管外的超流成分通过棉花塞向管内转移,形成内外压强差,液氦从喷嘴喷出。
第二声波 普通流体中的声波是由密度交替变化形成的,称密度波。1941年朗道发展了量子液体的流体动力学,预言在HeⅡ中除普通密度波(称第一声波)外,还存在另一种声波,它是由液氦中超流成分(低熵,温度较低)与正常流体成分(高熵,温度较高)的相对运动形成的,称为温度波或熵波(第二声波)。实验证实了温度波的存在。 3He是4He的同位素,在天然氦中所占比例小于10-7,通过人工核反应可得足够数量的3He。3He的临界温度和临界压强分别为3.34K和1.17大气压。与4He一样,在常压下液态3He不会固化,在绝对零度附近需加34个大气压才能固化。1972年,D.D.奥舍罗夫等人在2mK低温下发现了两个3He的液态新相,分别称为3He-A和3He-B,它们均为超流态。液态3He和4He在0.87K以上温度时完全互溶,在该温度以下则分离成两相,按3He所占比例的多少分别称为浓相(含3He较多)和稀相(含3He较少),浓相浮于稀相之上(因3He比4He轻)。3He原子从浓相通过界面进入稀相时要吸热,这就是稀释致冷机的工作原理(见超低温技术)。3He原子的电子总自旋为零,核自旋为1/2,故与电子一样属费米子,遵守费米-狄拉克统计,液态3He称为费米液体,正常态的液态3He的性质可用朗道的费米液体理论描述。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条