1) complex viscosity
复数黏度
1.
The results showe that the elastic modulus(G'),viscous modulus(G″) and complex viscosity(η*) of collagen increase with increase of concentration,especially when collagen with a high concentration.
结果表明:随着浓度的增大,胶原溶液的弹性模量(G′)、粘性模量(G″)和复数黏度(η*)都提高,并且出现假固态行为,当胶原溶液浓度大于0。
2) pasting parameter
黏度参数
3) viscosity index
黏度指数
1.
Based on the problems of low viscosity index and the acidity increasing in the lubricating base oil,it has been found that the unstable quality of the crude oil was the root cause to effect on the quality of the base oil by analysis for long time;the low viscosity index and the higher acidity were resulted from the low paraffinicity and the high content of aromatics,cyclane.
针对润滑油基础油相继出现的黏度指数降低、酸值升高等问题,跟踪分析了润滑油基础油质量,认为原油的变化是造成润滑油基础油质量变化的根本原因;基础油组成中烷烃含量降低,芳烃和环烷烃含量上升是其酸值上升和黏度指数下降的内在原因。
2.
9%,the viscosity index was 23.
9%,黏度指数为23。
3.
The influence of different mass fraction of Cu-Ni-Sn nano-particles,SiO2 nano-particles,ultra-fine serpentine powders on base oil viscosity and viscosity index(VI) was discussed by Ping’s capillary viscometer.
采用综合热分析仪测试纳米铜、镍、锡和SiO2粉以及超细蛇纹石粉的差热分析曲线,研究了常用固体润滑添加剂的热稳定性,并用平氏毛细管黏度法研究了含不同质量分数纳米金属Cu-Ni-Sn粉、纳米SiO2粉和超细蛇纹石粉对基础油黏度及黏度指数的影响。
4) viscosity coefficient
黏度系数
5) viscosity function
黏度函数
6) inherent viscosity
比浓对数黏度
1.
The effects of dissolving on the structure and thermal properties of PPTA through IR spectra and TG were studied and the inherent viscosity and its relative molecular weight of PPTA solution with the influence of kinds of factors including dissolution time,solution temperature,concentration of the solution,concentration of strong sulfuric acid and stirring speed of twin screw were discussed.
分析溶解时间、温度、溶液质量分数、硫酸质量分数、双螺杆转速等溶解条件对PPTA的比浓对数黏度ηinh、相对分子质量的影响。
2.
The factors that may cause degradation of poly(p-phenylene terephthalamide)(PPTA) during preparation were studied by measuring the inherent viscosity.
通过测量不同条件下聚对苯二甲酰对苯二胺(PPTA)溶液的比浓对数黏度,分析在PPTA纺丝前可能引起聚合物降解的因素,这些因素包括纺丝液浓度、残余的CaCl2、N-甲基-2-吡咯烷酮、水分和氢氧化钙等,最终得到水分和氢氧化钙对PPTA的降解影响很大,其余影响较小的结论。
补充资料：复数
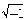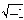| 复数 complex number 形如a＋bi的数。式中a，b 为实数，i是 一个满足i2＝－1的数，因为任何实数的平方不等于－1，所以i不是实数，而是实数以外的新的数。在复数a＋bi中，a 称为复数的实部，b称为复数的虚部，i称为虚数单位。当虚部等于零时，这个复数就是实数；当虚部不等于零时，这个复数称为虚数，虚数的实部如果等于零，则称为纯虚数。由上可知，复数集包含了实数集，因而是实数集的扩张。 复数的产生来自解代数方程的需要。16世纪，意大利数学家G.卡尔达诺首先用公式表示出了一元三次方程的根，但公式中引用了负数开方的形式，并把i＝  当作数，与其他数一起参与运算。由于人们无法理解 的实质，所以在很长时间内不承认负数的平方根也是数，而称之为虚数。直到19世纪，数学家们对这些虚数参与实数的代数运算作出了科学的解释，并在解方程和其他领域中使虚数得到了广泛的应用，人们才认识了这种新的数。复数的四则运算规定为： （a＋bi）＋（c＋di）＝（a＋c）＋（b＋d）i， （a＋bi）－（c＋di）＝（a－c）＋（b－d）i， （a＋bi）·（c＋di）＝（ac－bd）＋（bc＋ad）i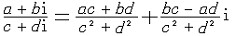，  （c与d不同时为零）。复数有多种表示形式，常用形式z＝a＋bi叫做代数式。此外有下列形式。 ①几何形式。复数z＝a＋bi 用直角坐标平面上点Z（a，b）表示。这种形式使复数的问题可以借助图形来研究。也可反过来用复数的理论解决一些几何问题。 ②向量形式。复数z＝a＋bi用一个以原点O为起点，点Z（a，b）为终点的向量OZ表示。这种形式使复数的加、减法运算得到恰当的几何解释。 ③三角形式。复数z＝a＋bi化为三角形式 z＝｜z｜（cosθ＋isinθ） 说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |